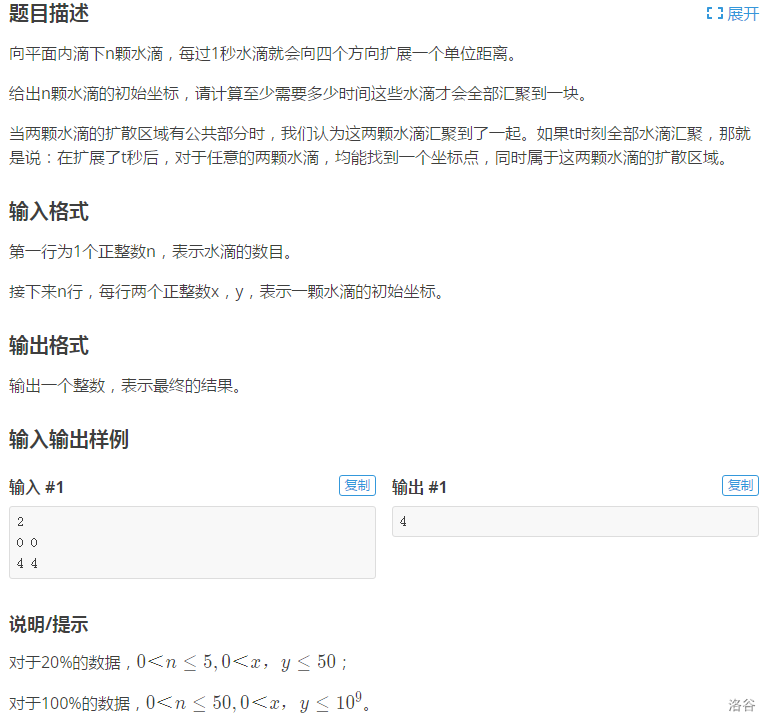
我的思路：将所有两个水滴之间的汇集时间求出来存入一个数组（代码中的k），其中n1与n2为水滴序号，再将这个数组从小到大排序（详见cmp函数），最后用并查集来判断水滴是否全部汇合（判断方式：最远的两滴水滴在同一个集合里）

结果：90分，WA一个

代码

#include<bits/stdc++.h>
using namespace std;

struct node{
	long long time,n1,n2;
}k[3600];

bool cmp(node c1,node c2){
	if(c1.time<c2.time)return 1;
	return 0;
}

long long n,x[60],y[60],father[6000],t,mint,ans,jlx,jly;

long long find(long long x)
{
	if(father[x]==x)return x;
	return father[x]=find(father[x]);
}

long long add(long long x,long long y)
{
	father[find(y)]=find(x);
}

int main()
{
	cin>>n;
	for(long long i=0;i<n;i++){
		cin>>x[i]>>y[i];
		father[i]=i;
	}long long jsq=0;
	for(long long i=0;i<n-1;i++){
		for(long long j=i+1;j<n;j++){
			k[jsq].n1=i;
			k[jsq].n2=j;
			jlx=abs(x[i]-x[j]);
			jly=abs(y[i]-y[j]);
			if(jlx%2==1){
				jlx++;
				jly--;
			}
			t=jlx/2;
			if(jly%2==1)jly++;
			t+=jly/2;
			k[jsq].time=t;
			jsq++;
		}
	}sort(k,k+jsq,cmp);
	long long abc;
	for(abc=0;abc<jsq;abc++){
		add(k[abc].n1,k[abc].n2);
		if(k[abc].time==k[abc+1].time)continue;
		if(find(k[jsq-1].n1)==find(k[jsq-1].n2))break;
	}cout<<k[abc].time;
	return 0;
}

另外如果谁知道洛谷上有这道题，帮忙发一下，谢谢